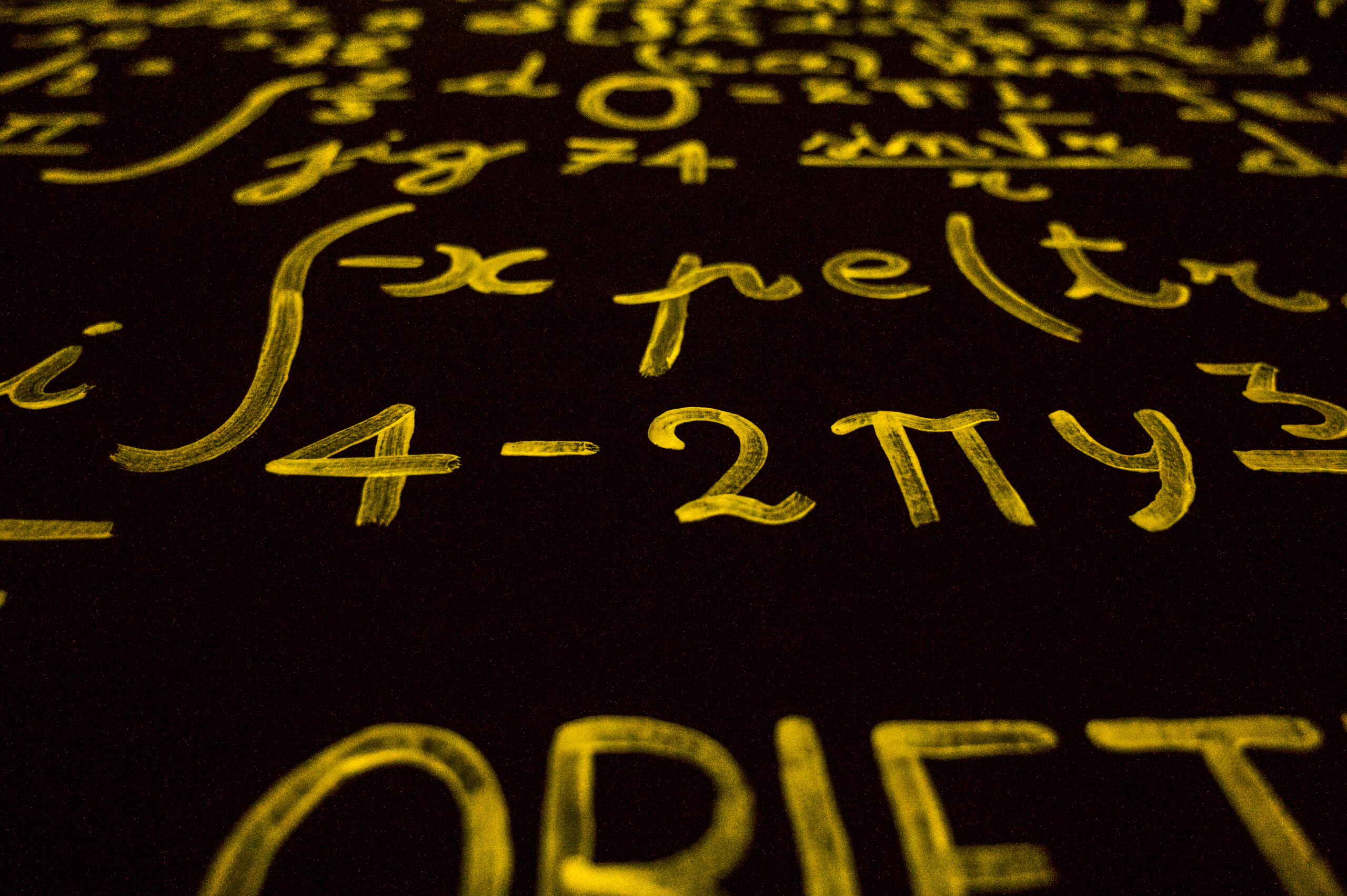La matematica è una disciplina che ha affascinato l’umanità per millenni, e molte delle sue scoperte fondamentali risalgono a tempi antichi. Anche se oggi ci troviamo circondati da tecnologie avanzate che si basano su complessi calcoli matematici, è sorprendente pensare che molte delle basi di questa scienza fossero già comprese migliaia di anni fa. Gli antichi Egizi, ad esempio, sapevano calcolare il volume di una piramide, mentre i Greci riuscirono a determinare l’area di un cerchio. Queste scoperte, se viste nel contesto storico, sono altrettanto impressionanti quanto le teorie di Einstein o Newton.
La nostra società moderna, con i suoi computer digitali e motori a combustione interna, si fonda sull’esplorazione dei numeri. Fortunatamente per noi, i matematici hanno iniziato questo viaggio molto tempo fa. David Burton, un professore dell’Università del New Hampshire, ha scritto che, con l’eccezione dell’astronomia, la matematica è la più antica e continua delle scienze esatte. Esploriamo alcune delle più grandi conquiste matematiche dell’antichità, tratte dai primi scritti sull’argomento.
Volume di una Piramide Tronca
La matematica è ovunque intorno a noi, dalle torri dei grattacieli ai ponti sospesi. Tuttavia, poche strutture ispirano meraviglia come la Piramide di Giza. Costruita circa 4.600 anni fa, questa meraviglia architettonica dimostra il potere del calcolo come nessun’altra opera del mondo antico.
Calcolare il volume di una piramide intera è relativamente semplice: basta prendere un terzo dell’area della base e moltiplicarlo per l’altezza. Questo si può facilmente dimostrare con modelli in miniatura di una piramide e di un prisma, entrambi con la stessa area di base e altezza. Riempendo la piramide con acqua e versandola nel prisma, si scopre che il prisma contiene esattamente tre volte il volume della piramide. Poiché il volume di un prisma è semplicemente base per altezza, si può dedurre il volume di una piramide.
La Formula della Piramide Tronca
La formula per il volume di una piramide tronca, ovvero una piramide con la cima tagliata, è molto più complessa. Gli Egizi non la scrivevano come facciamo noi oggi, ma il Papiro di Mosca, una raccolta di problemi matematici risalente al 1850 a.C., dimostra che avevano compreso il principio sottostante. Questo risultato era così avanzato per il suo tempo che Burton lo definì “il capolavoro della geometria antica”. Da un punto di vista pratico, permetteva loro di calcolare, durante la costruzione, quanto materiale fosse necessario per completare l’opera.
Impatto Pratico
La capacità di calcolare il volume di una piramide tronca non era solo un esercizio teorico. Aveva applicazioni pratiche significative, specialmente nella costruzione di monumenti e strutture. Gli Egizi potevano stimare con precisione la quantità di pietra necessaria per completare una piramide, ottimizzando così le risorse e il tempo impiegato nella costruzione. Questo tipo di calcolo era essenziale per la gestione dei progetti di costruzione su larga scala, che richiedevano una pianificazione meticolosa e una gestione efficiente delle risorse.
Il Teorema di Pitagora
Se c’è un concetto che molti ricordano dalle lezioni di geometria, è il teorema di Pitagora. In un triangolo rettangolo, il quadrato dell’ipotenusa, il lato più lungo, è uguale alla somma dei quadrati degli altri due lati. Questo teorema può essere verificato disegnando letteralmente quadrati che si estendono da ciascun lato del triangolo.
Origini del Teorema
Sebbene il teorema porti il nome del matematico greco Pitagora, che visse nel VI secolo a.C., le sue origini sono molto più antiche. Gli stessi Greci credevano che il teorema fosse stato tramandato loro dagli Egizi, e l’archeologia moderna supporta in gran parte questa affermazione. Tuttavia, i primi a scoprire questo gioiello geometrico furono i Babilonesi. Una tavoletta di argilla risalente al 1800 a.C., conosciuta come Plimpton 322, contiene una lista di terne pitagoriche, gruppi di tre numeri interi che soddisfano il teorema.
Applicazioni Pratiche
Molti studiosi hanno considerato la lista di Plimpton 322 come un esercizio di matematica teorica pura, forse un insieme di problemi utilizzati per insegnare agli studenti. Tuttavia, nel 2021, il matematico Daniel Mansfield dell’Università del New South Wales ha proposto un’interpretazione più pratica: questo “studio dei rettangoli” sembra essere nato dai problemi affrontati dai topografi mesopotamici nella misurazione del terreno. In un poema dello stesso periodo di Plimpton 322, un topografo riferisce che “quando uomini ingiustamente offesi hanno una disputa, io calmo i loro cuori.”
La Formula Quadratica
La formula quadratica è un altro pilastro dell’algebra, uno dei primi veri ostacoli che gli studenti delle scuole superiori incontrano. Anche se può sembrare intimidatoria, i Babilonesi non trovavano particolari difficoltà nell’affrontarla. Forse perché non la consideravano in termini così astratti come facciamo noi oggi.
Approccio Babilonese
I Babilonesi non avevano ancora inventato termini indefiniti come “a”, “b” e “c”, quindi usavano parole come “larghezza”, “lunghezza”, “area” e “volume”. Come il teorema di Pitagora, la formula quadratica aiutava nelle questioni amministrative pratiche. Tuttavia, molti dei problemi incisi nelle tavolette babilonesi sembrano essere esercizi intellettuali, piuttosto che trattati su topografia o contabilità, indicando un interesse astratto per le relazioni numeriche. Già allora, le persone cominciavano a vedere la matematica come un fine in sé.
Interesse Astratto
L’interesse per la matematica come disciplina astratta è evidente nei problemi matematici babilonesi. Anche se molti di questi problemi avevano applicazioni pratiche, come la misurazione del terreno o la gestione delle risorse, c’era anche un chiaro desiderio di esplorare le relazioni numeriche per il puro piacere della scoperta. Questo interesse per la matematica come disciplina teorica ha gettato le basi per lo sviluppo della matematica come la conosciamo oggi, una scienza che esplora le relazioni numeriche e geometriche in modo astratto e rigoroso.
Il Teorema di Talete
È giunto il momento di riconoscere il contributo dei Greci. Tra le numerose innovazioni geometriche, scoprirono un fatto estremamente interessante: se si costruisce un triangolo utilizzando il diametro di un cerchio come uno dei lati, gli altri due lati, se si incontrano sulla circonferenza del cerchio, formeranno sempre un angolo retto.
Dimostrazione e Impatto
Anche se oggi può sembrare un concetto semplice, nel VI secolo a.C. Talete e i suoi contemporanei stavano inventando la matematica dimostrativa da zero, utilizzando il ragionamento logico per scoprire verità inconfutabili sul mondo. Talete potrebbe aver appreso il contenuto del suo teorema durante un viaggio a Babilonia, ma fu lui (almeno secondo la tradizione) a fornirne una dimostrazione rigorosa. Questo è ciò che lo rende un “teorema”, non solo un trucco da festa.
Contributo alla Matematica
Per questo motivo, Talete è spesso celebrato come il primo vero matematico, l’ideatore dell’organizzazione deduttiva della geometria. Non possiamo essere certi di chi abbia realmente formulato questo teorema. Talete era un favorito, così come Pitagora. Ma poiché quest’ultimo riceve il merito per l’equazione più famosa dell’antichità, lasciamo che Talete abbia questo riconoscimento.
Il Problema del Bestiame di Archimede
Alcuni secoli dopo Talete, il matematico greco per eccellenza era Archimede. Quando non era impegnato a rivoluzionare la geometria e a inventare nuovi strumenti ingegnosi, si divertiva con quelli che Burton definiva “problemi aritmetici vestiti in abiti poetici”. Traeva ispirazione per uno di questi problemi da una linea dell’Odissea: “Poi raggiungerai l’isola di Trinacria, dove in gran numero pascolano molti buoi e pecore grasse del Sole.”
Il Dilemma di Archimede
Archimede voleva sapere quanti buoi ci fossero. La domanda, come la pose, era estremamente complicata, ma in sostanza si riduceva alla differenza tra due quadrati, che può essere rappresentata così. Oggi questo è noto come un’equazione di Pell, erroneamente chiamata così per il matematico inglese John Pell, anche se arrivò 2.000 anni dopo. Detto ciò, Archimede e altri primi investigatori di tali equazioni non erano attrezzati per risolverle. Anche se non poteva saperlo all’epoca, il suo enigma originale chiede la soluzione a un problema che richiede un calcolo complesso.
Influenza Duratura
La risposta, finalmente raggiunta nel 1965 con l’aiuto di un computer, si estende per 206.545 cifre. Per quanto riguarda Archimede e i suoi contemporanei, Burton scrisse che “probabilmente mostrarono le equazioni coinvolte e lasciarono la questione a quel punto”. Tuttavia, ciò non sminuisce la forza immaginativa necessaria solo per formulare la domanda. Le equazioni di Pell hanno affascinato molte delle menti matematiche più grandi dell’era moderna, da Pierre de Fermat a Leonhard Euler. Prima di loro, i matematici indiani Brahmagupta e Bhāskara II (vissuti rispettivamente nel VII e XII secolo d.C.) scoprirono algoritmi per trovare soluzioni intere a queste equazioni. E ancora oggi le persone continuano a esplorare i loro punti più sottili, formando un filo conduttore accademico che risale fino ai tempi antichi.